3D Projectile Motion
Skills: MATLAB, Kinematics, trajectory generation
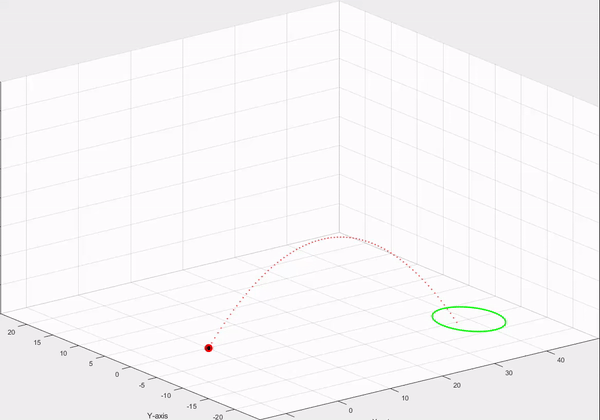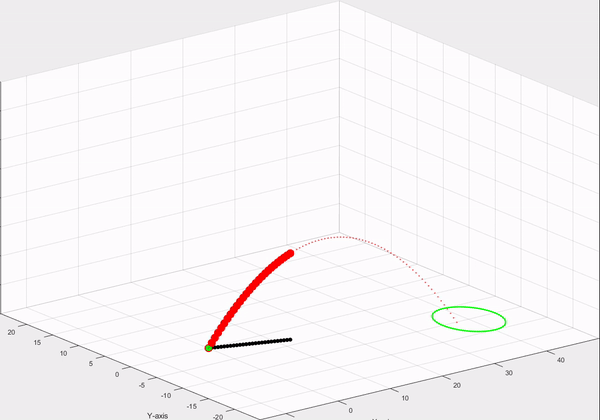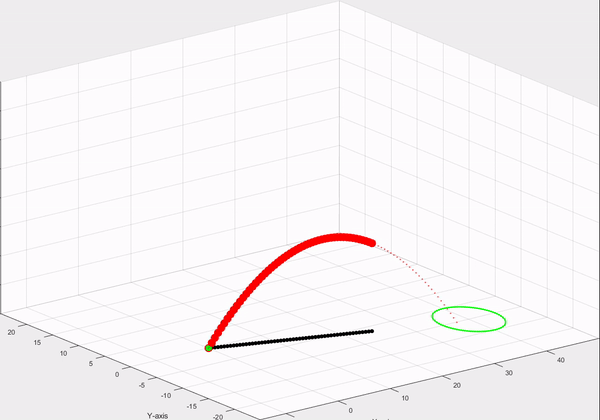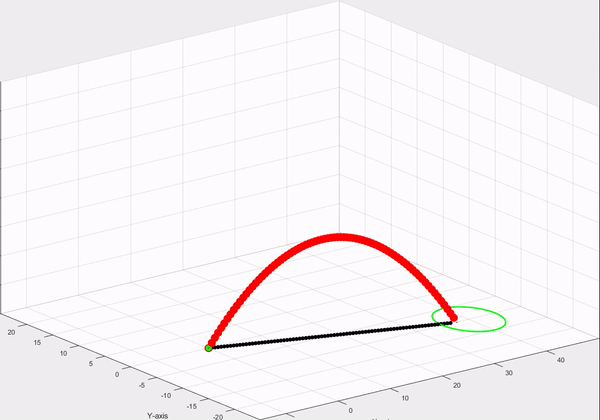
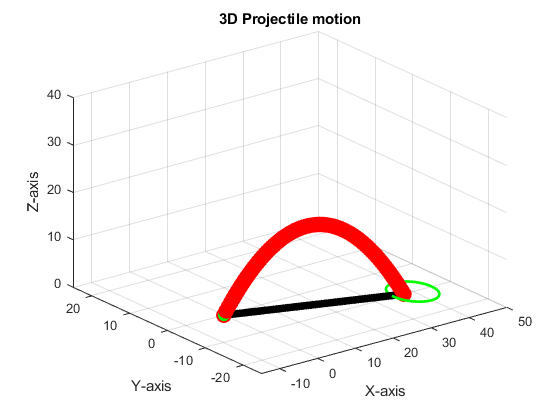
Demo:
Projectile Model:
“A projectile motion is a motion where a ball is fired in the air at an angle and is allowed to moved under the force of gravity”. I woke up one morning and remembered this definition from my physics teacher in secondary school. As an engineering student, I wanted to vizualize it once more using a software tool like Matlab, as these fundamental concepts never dies once you grasp it.
Goal
The goal of this experimentation was to shoot a sperical projectile (ball, stone, etc.) and control it with the help of inputs to achieve a desired location. Then the projectile flies according to the laws of physics and thus accelerated by the force of gravity to the ground.
Inputs:
- Initial Velocity: $v_0$
- Angle from x-y plane: $\theta$
- Angle from x-axis: $\phi$
output
- To graphically visualise the trajectory from start to target point.
Equation of motion:
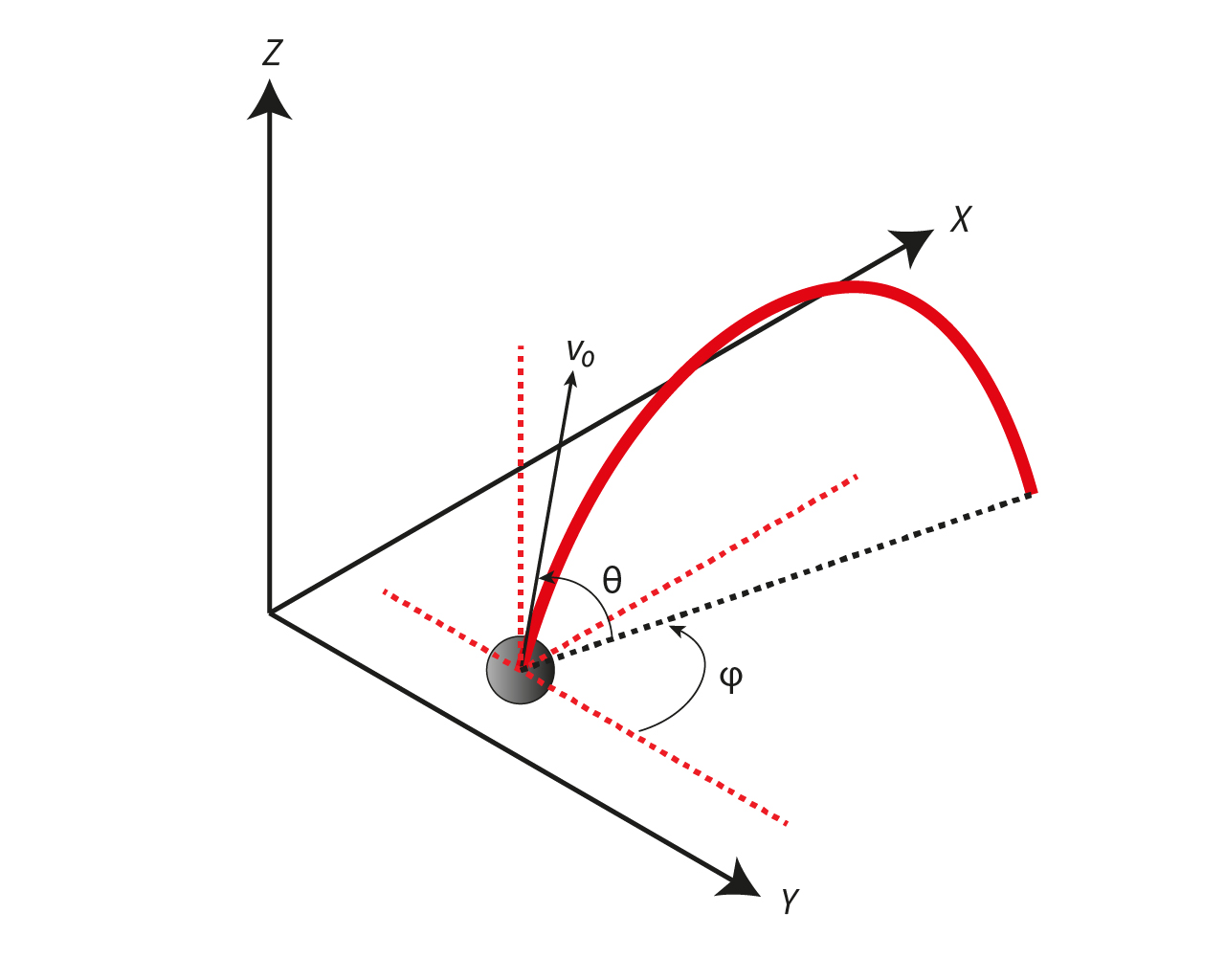
From the free body diagram above, the equation of motion was evaluated in vector and each component is independent. Therefore they can be written as;
- x-direction: $m\frac{d^2}{dt^2}x(t) = 0$
- y-direction: $m\frac{d^2}{dt^2}y(t) = 0$
- z-direction: $m\frac{d^2}{dt^2}z(t) = -mg_z$
Intergrating twice the above equation yield
- $x(t) = x_0 + v_{x,0}t$
- $y(t) = y_0 + v_{y,0}t$
- $z(t) = z_0 + v_{z,0}t - \frac{1}{2}gt^2$
Once more specifying the initial positions (x_0,y_0,z_0) in order to compute the inital velocity $v_0$,
- $v_{0,x} = v_0cos(\phi)cos(\theta)$
- $v_{0,y} = v_0sin(\phi)cos(\theta)$
- $v_{0,x} = v_0sin(\theta)$
After jumping into Matlab and spending most of the time to visualise, The result was quite satisfactory. The matlab code is displayed below as follows.
Matlab Script:
%% Projectile motion
clc; clear; close;
%% Shooter parameters
params = sys_params; g = params.gravity;
% maximum number of points for simulation
nmax = 80;
% initial conditions
p0 = [0; 0; 0];
phi = -15; % from -90 to 90
theta = 60; % from 0 to 90
v0 = 21;
% desired position
pd = [40; -10; 0];
% time required to hit the ground
tmax = (2*v0*sind(theta))/g;
[t,X] = myFlightModel(phi, theta, p0, v0, tmax, nmax);
%% target circle
% Define the center and radius of the circle
centerX = pd(1); % x-coordinate of the center
centerY = pd(2); % y-coordinate of the center
radius = 5; % radius of the circle
% Generate points along the circumference of the circle
alpha = linspace(0, 2*pi, 100); % Generate 100 points around the circle
x = centerX + radius * cos(alpha);
y = centerY + radius * sin(alpha);
z = zeros(size(x)); % Z-coordinates are all zero for the XY plane
%% Plot
for i=1:nmax
% 3D scatter plot with initial condition
plot3(p0(1), p0(2), p0(3),'.g','markersize',30);
hold on;
% target circle
plot3(x, y, z, 'g','LineWidth',2);
hold on;
% plot trajectory
ball = plot3(X(1,i),X(2,i),X(3,i),'.r','markersize',40);
% draw path
plot3(X(1,:),X(2,:),X(3,:), '.r','markersize',5);
% draw shadow
shadow = plot3(X(1,i),X(2,i),0*X(3,i), '.k', 'markersize',20);
if i >= nmax-1
delete(shadow); % Clear the last 2 plot
end
% draw desired point
% plot3(pd(1), pd(2), pd(3),'.g','markersize',30);
grid on; % Display the grid
% Label the axes
xlabel('X-axis'); ylabel('Y-axis'); zlabel('Z-axis');
% Set the plot title
title('3D Projectile motion');
axis([-15,50,-25,25,0,40])
set(gca,"Clipping","off")
drawnow;
end
%% Projectile function
function [t,X]=myFlightModel(phi, theta, p0, v0, tmax, nmax)
t=linspace(0,tmax,nmax);
%--------------------------------------
params = sys_params; g = params.gravity;
x0 = p0(1); y0 = p0(2); z0 = p0(3);
v_x0 = v0*cosd(theta).*cosd(phi);
v_y0 = v0*cosd(theta).*sind(phi);
v_z0 = v0*sind(theta);
x = x0 + v_x0*t; y = y0 + v_y0*t; z = z0 + v_z0*t - 0.5*g*t.^2;
X=[x;y;z];
% --------------------------------------
end
%% system parameters
function [ params ] = sys_params()
% Physical properties
params.gravity = 9.81;
params.mass = 0.0638;
params.arm_length = 0.086;
% Actuator limits
params.u_min = 0;
params.u_max = 1.2*params.mass*params.gravity;
end
